Clojureのincanter(統計解析用のライブラリ)が使えるようになったので, とりあえず, クラスタリングをやってみました. Single Linkage (単連結法)および, Complete Linkage(完全連結法)は, 階層的クラスタリングの手法の一種で, 距離空間に散らばった多数の点をその位置からそれぞれグループ(クラスタ)ごとに分類する手法です.
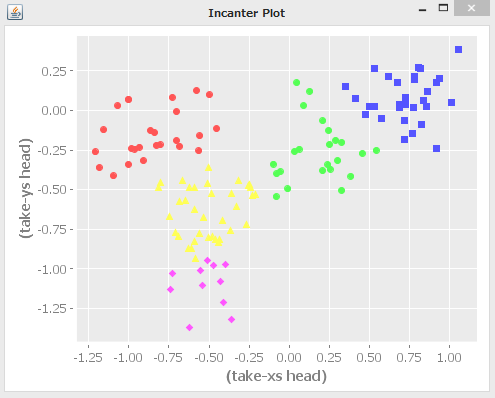
例えば, 下の図は, 5つのガウス分布に従ってプロットされた二次元上の点です (各ガウス分布ごとに色で分類されています).
これをComplete Linkageによって, 5つのクラスタへ分類すると, 次のようになります.
元のガウス分布にいくらか従いながら, 近い(近そうな)点どうしが, それぞれのクラスタとして, ひとまとめにされていることが観察できると思います.
クラスタリングでは, 空間上の点の位置を元にして同じようなどうしを一つにまとめ, 元の分布を予測したり, グループごとに分類します.
データクラスタの可視化
incanterでは, 二次元空間上のグラフのプロットや行列の処理が簡単に使えるので, このようなクラスタリングが, 簡単に実装できます.
(require '[incanter.core :as core]
'[incanter.stats :as st]
'[incanter.charts :as ch]
'[clojure.math.numeric-tower :as tower])
;; ------------------------- ------------------------- -------------------------
;; show clusters
;; ------------------------- ------------------------- -------------------------
(defn plot-with-clusters [clusters] ;; clusters = [[[x1 y1] [x2 y2] ...] ...]
(let [head (first clusters)
init-plot (ch/scatter-plot (map first head) (map second head))]
(reduce #(ch/add-points %1 (map first %2) (map second %2))
init-plot (rest clusters)))) 名前の衝突を避けるためにrequireでincanterをロードします. incanterではscatter-plotで点を二次元座標上にプロットできます(一番目のクラスタをscatter-plotでプロット). add-pointsでchartオブジェクトに点を付加, reduceで各クラスタを一つにまとめます.
サンプルとなるデータ点のリスト
これに, ランダムなパラメータを持つ複数のガウス分布に従うデータセットを作ります.
(defn generate-random-parameter []
{:sd (+ 0.15 (rand 0.1)) :x (dec (rand 2)) :y (dec (rand 2))
:size (+ 20 (rand-int 10))})
(defn generate-sample-set [parts]
(let [generate-by #(st/sample-normal (:size %1) :mean (%2 %1) :sd (:sd %1))]
(map (fn [p] (map list (generate-by p :x) (generate-by p :y)))
(take parts (repeatedly generate-random-parameter))))) sample-normalは, ガウス分布に従うサンプルデータを生成します. 標準偏差等のパラメータの範囲は適当です. generate-sample-setでサンプルのデータ点(x, y)のリストを生成します.
データ的には, [ [[0.1 0.2] [-0.3 0.1] ......] [[0.3 -0.02] ......] ......]のように, 各クラスタごとに(x, y)座標がひとつのリストに.
(coreの)view関数で, (scatter)プロットされたオブジェクトを表示できます.
user> (core/view (plot-with-clusters (generate-sample-set 3)))
このリストを(apply concat ls)で, 結合してサンプルのデータ点のリストを作ります. 何か面白いデータがあれば, それでクラスタリングができるのですが...... このデータ列が本来クラスタリングにより分析されるデータになります.
距離
距離空間には, マンハッタン距離やマハラノビス距離などありますが, 今回は典型的なユークリッド距離を使います. 簡単にいえば, 視覚的な距離がそのまま, データ間の距離になります.
(defn distance [x1 y1 x2 y2]
(double (tower/sqrt (+ (core/sq (- x1 x2)) (core/sq (- y1 y2))))))
(defn compare-pairs [xy1 xy2]
(distance (first xy1) (second xy1) (first xy2) (second xy2)))
Single Linkage, Complete Linkageと階層的クラスタリング
Single/Complete Linkageは, 階層的クラスタリングの一種です. 階層的クラスタリングとは, クラスタ群の中から2つクラスタを選びその2つを結合していき, 目標となるクラスタ数に達するまで結合を続けます. クラスタ群の初期状態では, データ点一つに対し, 一つクラスタを定義します. 階層的クラスタリングの欠点の一つは, 最終的なクラスタ数を指示する必要があることです. 最終的なクラスタ数の適切な値がわからない時にはこの設定が問題となります. しかし, 裏を返せば, 好きなようにクラスタ数を決められるということでもあります.
Single LinkageとComplete Linkageの違いは, クラスタ間の距離の定義です. Single Linkageでは, 2つのクラスタ間どうしで最も近い要素間の距離がそのクラスタ間の距離になります. 一方, Complete Linkageは, 最も遠い要素間の距離がクラスタ間の距離とします.
(defn single-linkage "cluster a & cluster b -> distance" [a b]
(reduce min (map #(reduce min (map (partial compare-pairs %) b)) a)))
(defn complete-linkage "cluster a & cluster b -> distance" [a b]
(reduce max (map #(reduce max (map (partial compare-pairs %) b)) a)))
プログラム上の違いはmin/maxだけですが, Single Linkageの考え方としては, 2つのクラスタが同じクラスタなら要素間に繋がりがあるはずだということで, Complete Linkageの方は, 同じクラスタに含まれるということは要素がそれなりに凝集しているはずだ, ということでしょう.
IncanterのMatricesと距離行列
incanterを使っていて, せっかくなので距離行列(クラスタ間の距離のデータを保存している行列)もincanterの行列を使いました.
Clojureのシーケンス(リスト)から, matrixオブジェクトを生成できます. 同じクラスタ群の距離を保存するための行列なので, 対象行列になり, 対格要素は0になります. ここでの計算において, 対格要素は使いませんが, わかりにくいので対格要素は無限大としました.
こんな感じ.
user> (generate-init-matrix (map (fn [x] [x]) (apply concat (generate-sample-set 5))))
A 118x118 matrix
-----------------
Infinity 1.79e-01 3.13e-01 . 1.96e+00 2.09e+00 2.26e+00
1.79e-01 Infinity 1.78e-01 . 1.85e+00 1.99e+00 2.14e+00
3.13e-01 1.78e-01 Infinity . 1.93e+00 2.08e+00 2.21e+00
...
1.96e+00 1.85e+00 1.93e+00 . Infinity 2.07e-01 3.39e-01
2.09e+00 1.99e+00 2.08e+00 . 2.07e-01 Infinity 3.69e-01
2.26e+00 2.14e+00 2.21e+00 . 3.39e-01 3.69e-01 Infinity
matrixオブジェクトは, デフォルトでtoStringメソッドが実装されているため, replでは, 間を省略した行列が表示されます. 上の例は, 対格要素をPOSITIVE_INFINITYにした118×118の行列. 巨大な行列でも間引かれているので表示されるときはコンパクトになります.
(def inf Double/POSITIVE_INFINITY)
(defn distances-xy-xys [xy xys]
(cons inf (map (fn [xy1] (compare-pairs (first xy) (first xy1))) (rest xys))))
(defn generate-init-matrix [xys]
(let [dist-vec (map distances-xy-xys (drop-last xys) (iterate rest xys))]
(core/symmetric-matrix
(apply concat (concat dist-vec [[inf]])) :lower false)))
(defn find-conj-pair [dist-matrix width]
(loop [x (dec width) y (dec width) conj-pair [width width] min-value inf]
(cond
(< y 0) conj-pair
(< x 0) (recur y (dec y) conj-pair min-value)
:else (let [value (core/sel dist-matrix :cols x :rows y)]
(if (< value min-value)
(recur (dec x) y [x y] value) ;; update pair
(recur (dec x) y conj-pair min-value)))))) ;; not update pair
(defn update-dists
"updates distance matrix
dist-matrix : distance matrix
i, j : delete target
new-column : newly generated distances from i,j"
[dist-matrix i j new-column]
(->> (core/sel dist-matrix :except-rows [i j] :except-cols [i j])
(core/bind-rows new-column)
(core/bind-columns (cons inf new-column)))) 上2つの関数は, 初期状態の距離行列を作るためのものです. find-conj-pairで距離行列から結合する2つのクラスタのペアをインデックスで返します. update-distsで距離行列を更新します. 新しく生成されたクラスタと他のクラスタ間の距離を行列の上の行(と左側の列)に付け加えて更新します.
階層的クラスタリング
クラスタ群は, 簡単のため, i,jのインデックスで扱います.
(defn remove-clusters [i j clusters]
(let [;; supposed to be c_0 c_1 ... c_n ... c_m ... c_max
n (min i j) m (max i j)
;; [[c_0 ... c_n ... c_m-1] [c_m ... c_max]]
first-m-last (split-at m clusters)
;; [[c_0 ... c_n-1] [c_n ... c_m-1]]
first-n-m (split-at n (first first-m-last))]
;; (concat [c_0 ... c_n-1] [c_n+1 ... c_m-1] [c_m+1 ... c_max])
(concat (first first-n-m) (rest (second first-n-m)) (rest (second first-m-last))))) remove-clustersでクラスタ群のi,j番目のクラスタを除去します.
以下は, クラスタリングのループです. 一番近いクラスタを探し出し, 結合して更新という処理を指定されたクラスタ数になるまで続けます.
(defn clustering [calc-dists xys target-size]
(loop [clusters (map (fn [x] [x]) xys)
dist-matrix (generate-init-matrix clusters)
cluster-size (count xys)]
(if (<= cluster-size target-size)
clusters
(let [conj-pair (find-conj-pair dist-matrix cluster-size)
i (first conj-pair) j (second conj-pair)
new-cluster (concat (nth clusters i) (nth clusters j))
other-clusters (remove-clusters i j clusters)]
(recur (cons new-cluster other-clusters)
(update-dists dist-matrix i j (calc-dists new-cluster other-clusters))
(dec cluster-size))))))
(defn link-with [dist-f new-cluster other-clusters]
(map (fn [cluster] (dist-f new-cluster cluster)) other-clusters))
(defn clustering-with-single-linkage [xys number-of-clusters]
(clustering (partial link-with single-linkage) xys number-of-clusters))
(defn clustering-with-complete-linkage [xys number-of-clusters]
(clustering (partial link-with complete-linkage) xys number-of-clusters))実行結果
こんな感じでサンプルのデータ点を生成して,
user> (def A (generate-sample-set 5))
user> (core/view (plot-with-clusters A))
こんな感じのガウス分布になっているものに, 最終的なクラスタ数を5に設定してSingle Linkageをつかうと,
user> (core/view (plot-with-clusters (clustering-with-single-linkage (apply concat A) 5)))
となり, 同様に最終的なクラスタ数を5に設定したComplete Linkageでは,
user> (core/view (plot-with-clusters (clustering-with-complete-linkage (apply concat A) 5)))
になります.
Complete Linkageの方が, うまく(?)クラスタリングされているように見えます. 元の分布を完全に予測しているわけではありませんが, 生成されたときの分布4に近いかたちで分類できています. Single Linkageは, 孤立した点が一つのクラスタに分類されてしまう傾向があるようです. 全体がほぼ2つのクラスタに分類されてしまっています.
参考文献
全ソースコード.
(require '[incanter.core :as core]
'[incanter.stats :as st]
'[incanter.charts :as ch]
'[clojure.math.numeric-tower :as tower])
;; ------------------------- ------------------------- -------------------------
;; show clusters
;; ------------------------- ------------------------- -------------------------
(defn plot-with-clusters [clusters] ;; clusters = [[[x1 y1] [x2 y2] ...] ...]
(let [head (first clusters)
init-plot (ch/scatter-plot (map first head) (map second head))]
(reduce #(ch/add-points %1 (map first %2) (map second %2))
init-plot (rest clusters))))
;; ------------------------- ------------------------- -------------------------
;; generate data set
;; ------------------------- ------------------------- -------------------------
(defn generate-random-parameter []
{:sd (+ 0.15 (rand 0.1)) :x (dec (rand 2)) :y (dec (rand 2))
:size (+ 20 (rand-int 10))})
(defn generate-sample-set [parts]
(let [generate-by #(st/sample-normal (:size %1) :mean (%2 %1) :sd (:sd %1))]
(map (fn [p] (map list (generate-by p :x) (generate-by p :y)))
(take parts (repeatedly generate-random-parameter)))))
;; ------------------------- ------------------------- -------------------------
;; clustering
;; ------------------------- ------------------------- -------------------------
(defn distance [x1 y1 x2 y2]
(double (tower/sqrt (+ (core/sq (- x1 x2)) (core/sq (- y1 y2))))))
(defn compare-pairs [xy1 xy2]
(distance (first xy1) (second xy1) (first xy2) (second xy2)))
(defn single-linkage "cluster a & cluster b -> distance" [a b]
(reduce min (map #(reduce min (map (partial compare-pairs %) b)) a)))
(defn complete-linkage "cluster a & cluster b -> distance" [a b]
(reduce max (map #(reduce max (map (partial compare-pairs %) b)) a)))
(def inf Double/POSITIVE_INFINITY)
(defn distances-xy-xys [xy xys]
(cons inf (map (fn [xy1] (compare-pairs (first xy) (first xy1))) (rest xys))))
(defn generate-init-matrix [xys]
(let [dist-vec (map distances-xy-xys (drop-last xys) (iterate rest xys))]
(core/symmetric-matrix
(apply concat (concat dist-vec [[inf]])) :lower false)))
(defn find-conj-pair [dist-matrix width]
(loop [x (dec width) y (dec width) conj-pair [width width] min-value inf]
(cond
(< y 0) conj-pair
(< x 0) (recur y (dec y) conj-pair min-value)
:else (let [value (core/sel dist-matrix :cols x :rows y)]
(if (< value min-value)
(recur (dec x) y [x y] value) ;; update pair
(recur (dec x) y conj-pair min-value)))))) ;; not update pair
(defn update-dists
"updates distance matrix
dist-matrix : distance matrix
i, j : delete target
new-column : newly generated distances from i,j"
[dist-matrix i j new-column]
(->> (core/sel dist-matrix :except-rows [i j] :except-cols [i j])
(core/bind-rows new-column)
(core/bind-columns (cons inf new-column))))
(defn remove-clusters [i j clusters]
(let [;; supposed to be c_0 c_1 ... c_n ... c_m ... c_max
n (min i j) m (max i j)
;; [[c_0 ... c_n ... c_m-1] [c_m ... c_max]]
first-m-last (split-at m clusters)
;; [[c_0 ... c_n-1] [c_n ... c_m-1]]
first-n-m (split-at n (first first-m-last))]
;; (concat [c_0 ... c_n-1] [c_n+1 ... c_m-1] [c_m+1 ... c_max])
(concat (first first-n-m) (rest (second first-n-m)) (rest (second first-m-last)))))
(defn clustering [calc-dists xys target-size]
(loop [clusters (map (fn [x] [x]) xys)
dist-matrix (generate-init-matrix clusters)
cluster-size (count xys)]
(if (<= cluster-size target-size)
clusters
(let [conj-pair (find-conj-pair dist-matrix cluster-size)
i (first conj-pair) j (second conj-pair)
new-cluster (concat (nth clusters i) (nth clusters j))
other-clusters (remove-clusters i j clusters)]
(recur (cons new-cluster other-clusters)
(update-dists dist-matrix i j (calc-dists new-cluster other-clusters))
(dec cluster-size))))))
(defn link-with [dist-f new-cluster other-clusters]
(map (fn [cluster] (dist-f new-cluster cluster)) other-clusters))
(defn clustering-with-single-linkage [xys number-of-clusters]
(clustering (partial link-with single-linkage) xys number-of-clusters))
(defn clustering-with-complete-linkage [xys number-of-clusters]
(clustering (partial link-with complete-linkage) xys number-of-clusters))